The science of signal sampling
Sampling requires you to convert an analogue signal into digital information and back again. We break down the theory.
The Nyquist-Shannon sampling theorem
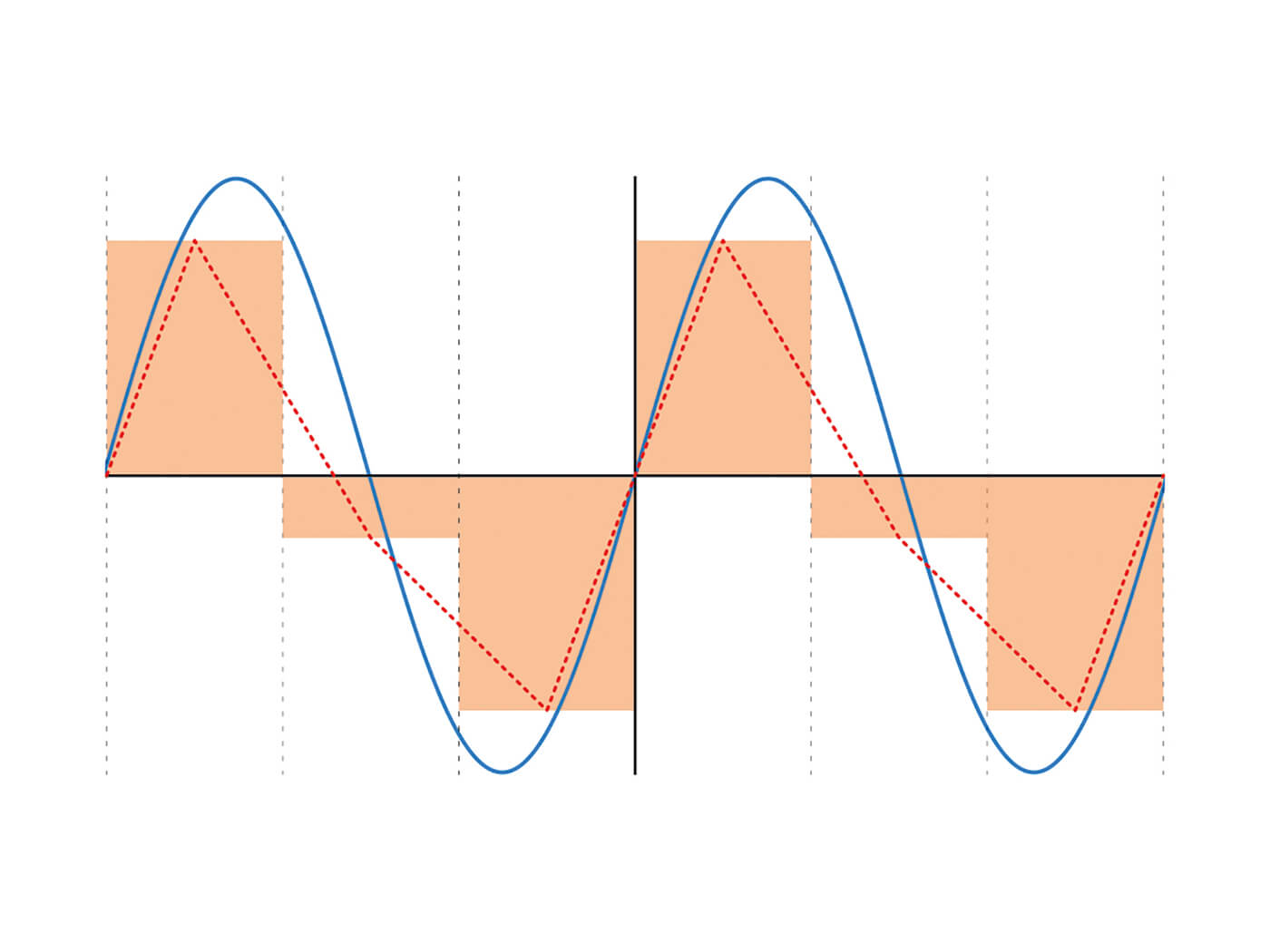
Audio sampling is rooted in digital-audio technology, the underlying principles of which were established as long ago as 1928 by electronics engineer Harry Nyquist and perfected in the late 1940s by mathematician, engineer and cryptographer Claude Shannon. The ideas these men established are now known as the Nyquist-Shannon Sampling Theorem, which is all about converting a continuous waveform into a series of discrete values from which the original waveform can be recreated.
Clearly, this is exactly what’s needed for turning analogue audio (a continuous waveform) into digital data (a series of discrete values) and back again.
The basic principle of signal sampling is very simple: it’s just a case of measuring a signal’s amplitude at regular time intervals. But the process of sampling and digitising an analogue waveform requires two significant approximations to be made. Firstly, the value that’s measured isn’t an instantaneous value, but is an average of the signal amplitude during the measurement time period. This means that finer details within that period will be lost.
Secondly, binary values have a ‘resolution’, or accuracy, that’s dictated by the number of data bits that are combined to represent the value, aka the byte size of the value; each ‘bit’ can have a value of zero or one and a byte combines a certain number of bits in order to represent a larger range of values. For example, an 8-bit byte can represent integer (whole number) values between 0 and 255 – that’s 256 possible values in all – and so any analogue value converted to an 8-bit byte value has to be rounded and approximated – or ‘quantised’ – onto this scale.�
What the Nyquist-Shannon Theorem allows us to do, then, is work out how frequently a source waveform has to be sampled, and how accurately its value has to be measured, in order for the original waveform to be reconstructed at a later date with an adequate degree of accuracy. In the recording studio, we know these factors as sample rate and bit depth, respectively.
Aliasing
Although modern digital-audio systems allow us to largely overlook these details, you may still find yourself working with a classic Akai MPC, E-MU Emulator, or whatever, where such considerations are vital to effective memory management. It’s also interesting to consider why the standard sample rates and bit depths that we use are what they are, so let’s dig a bit deeper into their impact on digital audio.
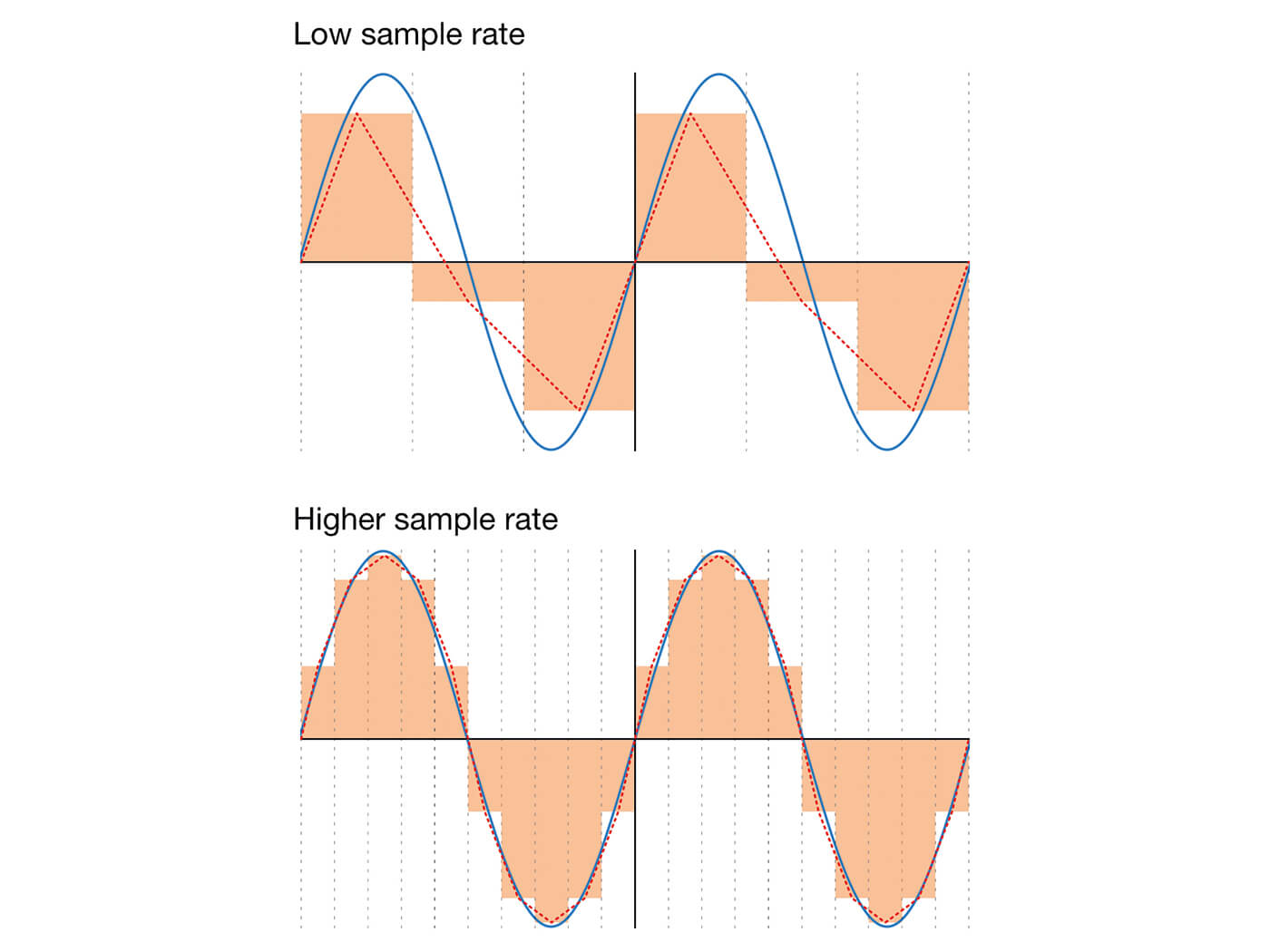
The sample rate determines the highest frequency that a digital audio system can capture accurately. This is because any amplitude changes – and therefore frequencies – within a source waveform that occur over a shorter period than the sampling period will be lost when the amplitude is measured. This leads to a form of waveform distortion known as ‘aliasing’, which manifests as a strange, high-pitched squeaking or warbling when the waveform is reconstructed.
The trick to avoiding aliasing is to ensure the sampling rate is high enough to capture all of the frequencies within the source sound (or all of those that you’re interested in, at least) and we can do this by calculating the ‘Nyquist Limit’ for the waveform and using this as our sampling rate. In essence, the Nyquist Limit is twice the highest frequency that one wants to capture, so if sampling a bass sound containing no frequencies above 10kHz, the Nyquist Limit – and therefore optimal sample rate for the sound – would be 20kHz.
However, even sounds that do most of their business at the low-frequency end of the audio spectrum can have harmonics that stretch a long way into the upper end. Often, such harmonics are adding little or nothing to the overall sound, but would cause audible aliasing if sampled at too low a rate.
The solution here is to pass the source sound through a low-pass filter prior to sampling, as this will remove those less important higher frequencies and thus allow the safe, aliasing-free use of lower sample rates. Doing this also makes it easy to judge the sample rate that should be used. For example, if you’re passing the source through a low-pass filter with a cutoff of, say, 5kHz, then you know the Nyquist Limit will be around 10kHz.
The Nyquist Limit is also the reason why so-called ‘CD quality’ audio has a sample rate of 44.1kHz: it is twice the 20kHz-or-so upper limit of human hearing. The even higher sample rates used in the studio allow even greater frequency accuracy and the ability to reproduce frequencies that are way beyond what the human ear can hear directly.
That’s not to say there’s no point using these high sample rates, though, as the point is that they capture of all the subtleties of the source waveform with a high degree of accuracy and banish any remaining aliasing to very high frequencies that will have no impact on the audible frequency band. In any event, this can be easily filtered out by a system’s digital-to-analogue converters.
Quantisation error
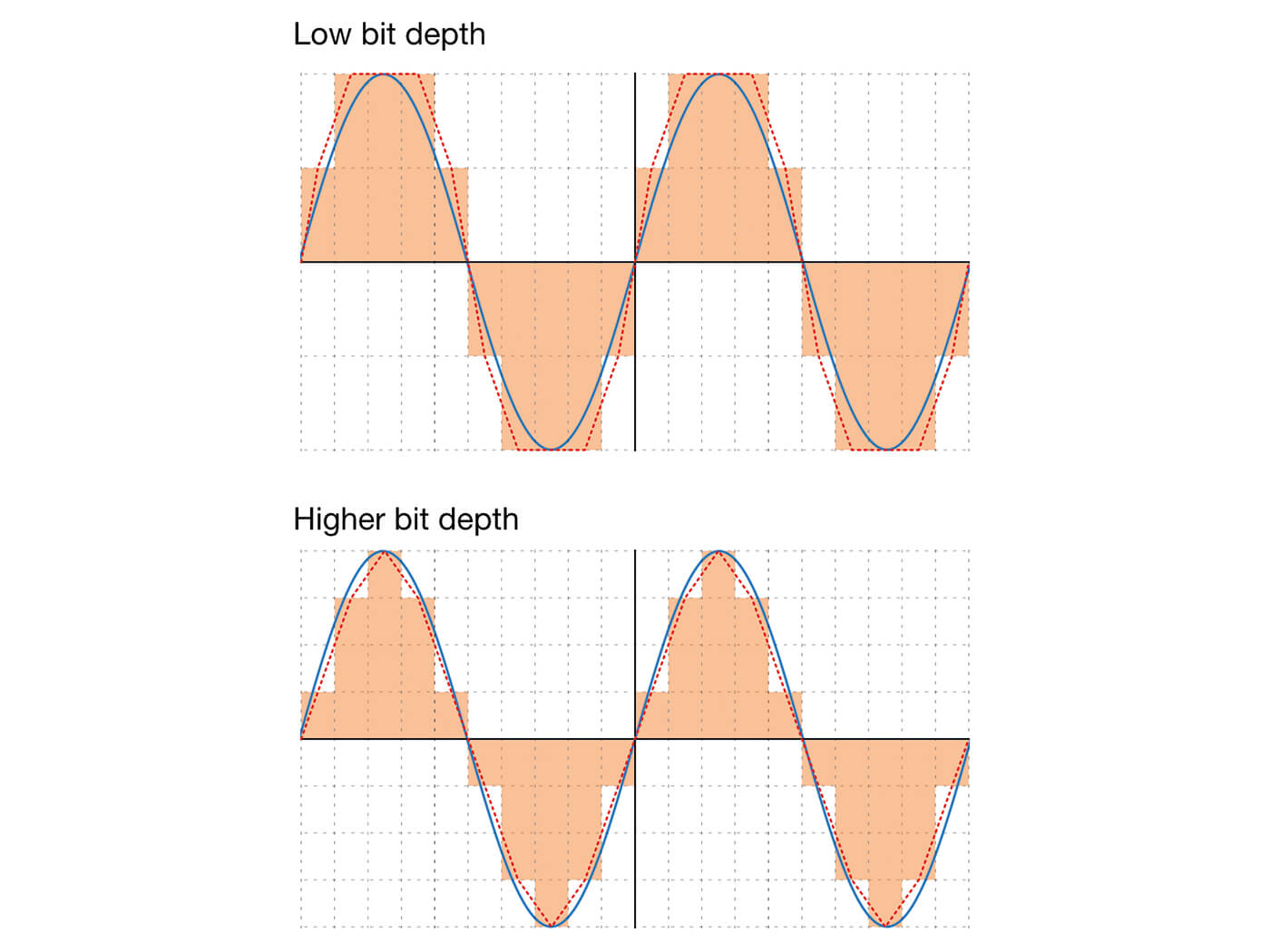
As already mentioned, the bit depth of a digital sample determines the range of values it can represent. Bearing in mind that a waveform fluctuates between negative and positive values, with an 8-bit signal full amplitude has a value of 0 or 255 depending on polarity, silence has a value of 127 (ie, the midpoint between 0 and 255) and all intervening values are quantised to this 0-255 scale.
Another way of thinking of this is that the bit depth determines the difference between the quietest and loudest signals within the system, otherwise known as the system’s dynamic range. In an 8-bit system, this is a mere 48dB. Upping to 16-bit gives a value range of 0 to 65,535 – a massive increase – and a resulting dynamic range of around 96dB. Moving to 24-bit gives 16,777,216 possible values and a dynamic range of 144dB.
As this shows, with each increase in bit depth the quantisation accuracy improves, but a tiny amount of inaccuracy will always remain. This inaccuracy is referred to as quantisation error and when audible, it sounds like a dirtiness or graininess in the reconstructed waveform. But again, as with the Nyquist Limit, the bit depth can be optimised based on the nature of the source; short sounds with little dynamic detail can be sampled at lower bit depths than those with greater dynamic detail.
Digital-to-analogue converters have various tricks up their sleeves to smooth-out and reduce the distortion caused by quantisation error, but it is always more noticeable at lower bit depths than higher ones.
Quantisation error can actually be quite a pleasing effect and it gave early 8- and 12-bit samplers, such as the Ensoniq Mirage and Akai S900 respectively, a certain sonic character that could be very satisfying – and that later 16-bit samplers lacked. These days, the same effect can be reproduced using a bitcrusher-style distortion effect.
Learn more about sample-based synthesis here.