Learning the basics of FM synthesis and how it works

Now that you’ve got some insight on the origins of FM synthesis, it’s time to understand how it works. Let’s break things down for you…

Partial to partials

If you were to remove all of the overtones from a waveform, so that all that was left was the fundamental frequency, you would have a sine wave; in other words, a sine wave is a pure tone with no overtones. Similarly, if you were to isolate any one overtone, it too would be a sine wave. Technically, each of these sine wave components is referred to as a partial. Taken to its logical conclusion, this means that all waveforms are made up of a stack of partials with differing frequencies and amplitudes.

Modulate not mix

FM synthesis harnesses this principle in order to generate complex waveforms from much simpler waveforms. But FM doesn’t just mix together those simple waveforms (although it can). Rather, it uses one simple waveform to modulate the frequency of another, with the result then being used to modulate another simple waveform, which in turn can modulate another, and so on.

The difference between modulation and simply mixing sine waves together is easiest to understand using the analogy of an imaginary guitar whose strings produce sine waves. When playing a chord on this guitar, each note of the chord would be a partial of the resulting waveform; changing notes would change the partial content and thus the timbre of the sound produced. 

When playing a single note on our imaginary guitar, you can add vibrato with your left hand. This modulates the pitch of the note at a frequency that’s independent of the note’s frequency, changing its waveform accordingly. If the vibrato rate were to be increased sufficiently, we would perceive timbral rather than pitch changes in the resulting sound. This is how FM works: it modulates the frequency of one waveform with another, and in so doing creates complexity in the resulting waveform.

The simple waveforms in an FM synth are produced by something called an ‘operator’. Operators are essentially just oscillators and the number available per-voice depends on the particular FM implementation; six-operator and four-operator are the most common variants. The simple waveforms an operator can produce also depends on the FM implementation, but for the purposes of this discussion, we’ll stick with sine-wave operators, as these are common to all implementations.

Operators are connected either to other operators, or to the synth’s output. The specific routing of these connections is referred to as an algorithm. The algorithm chosen for an FM patch has a huge impact on the resulting sound and it very much determines the type of sound a patch can produce – piano, strings, organ, or whatever.

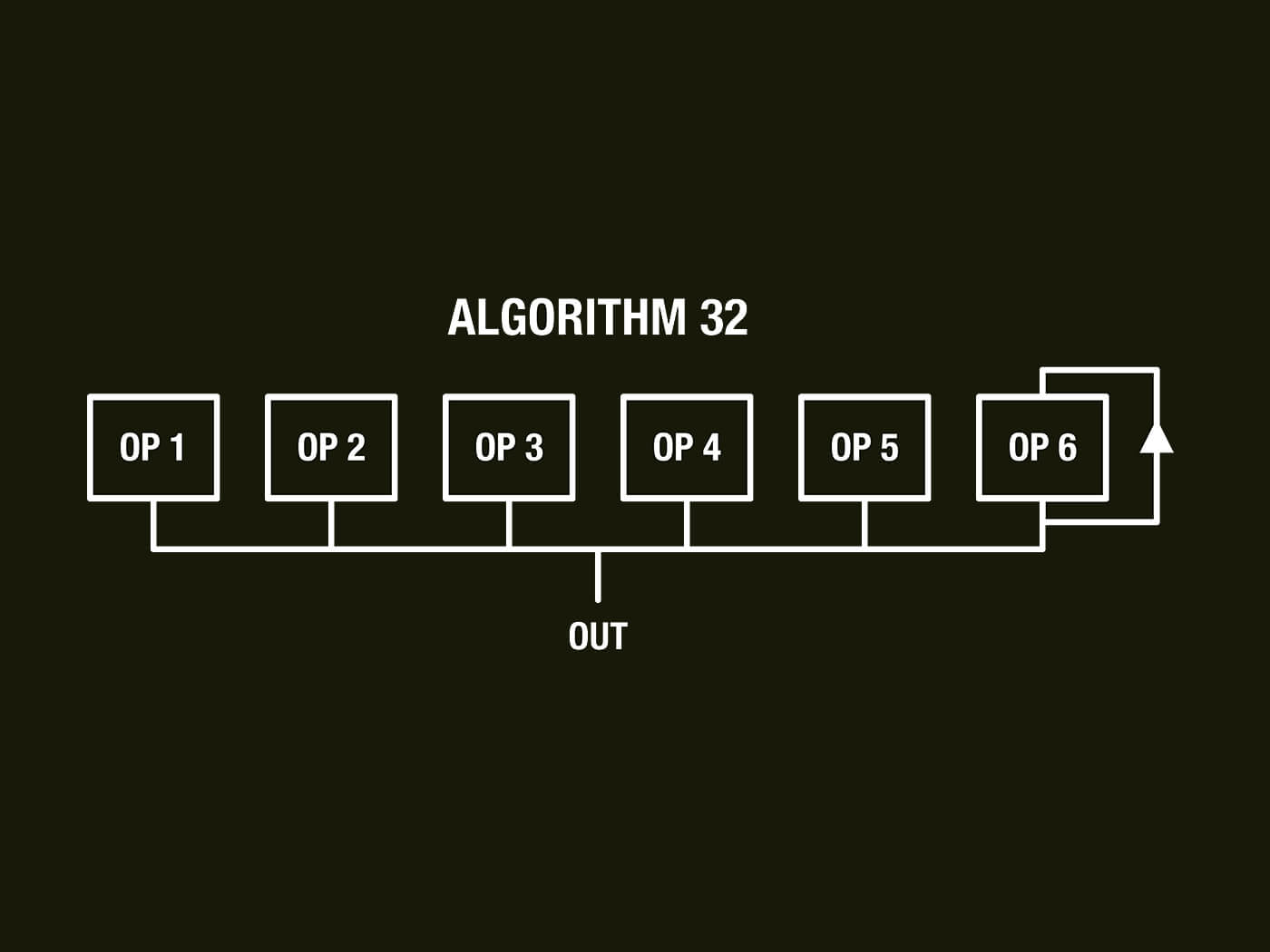
Operators connected to the output are called ‘carriers’ – these are the operators that you actually hear. Operators connected only to other operators are called ‘modulators’ and their output is not directly audible. Most algorithms also provide the facility for one operator to be fed back to an earlier point in the algorithm’s chain.

Making waves

There is a special category of partials called harmonics – and these are partials whose frequency is a multiple of the fundamental frequency: twice the fundamental frequency, three times the fundamental, four times and so on. Each ‘stop’ in this mathematical series is given a number: the fundamental frequency is also the first harmonic because it is 1x the fundamental frequency. The second harmonic is 2x the fundamental frequency, the third harmonic 3x and so on, ad -infinitum. Taken together, this is referred to as the ‘harmonic series’.

The geometric waveforms prevalent in all synthesis are special because their partials all fall within the harmonic series and the amplitude of those partials is based on the same mathematical relationship. 

For example, the partials of a square wave are the odd-numbered harmonics at amplitudes that are the inverse of the harmonic number. So the first partial is also the 1st harmonic and has a frequency of 1x the fundamental and an amplitude of 1/1 the fundamental. The second partial will be the 3rd harmonic with a frequency of 3x the fundamental and an amplitude 1/3rd that of the fundamental. The third partial will be the 5th harmonic at 1/5th the amplitude and so on.

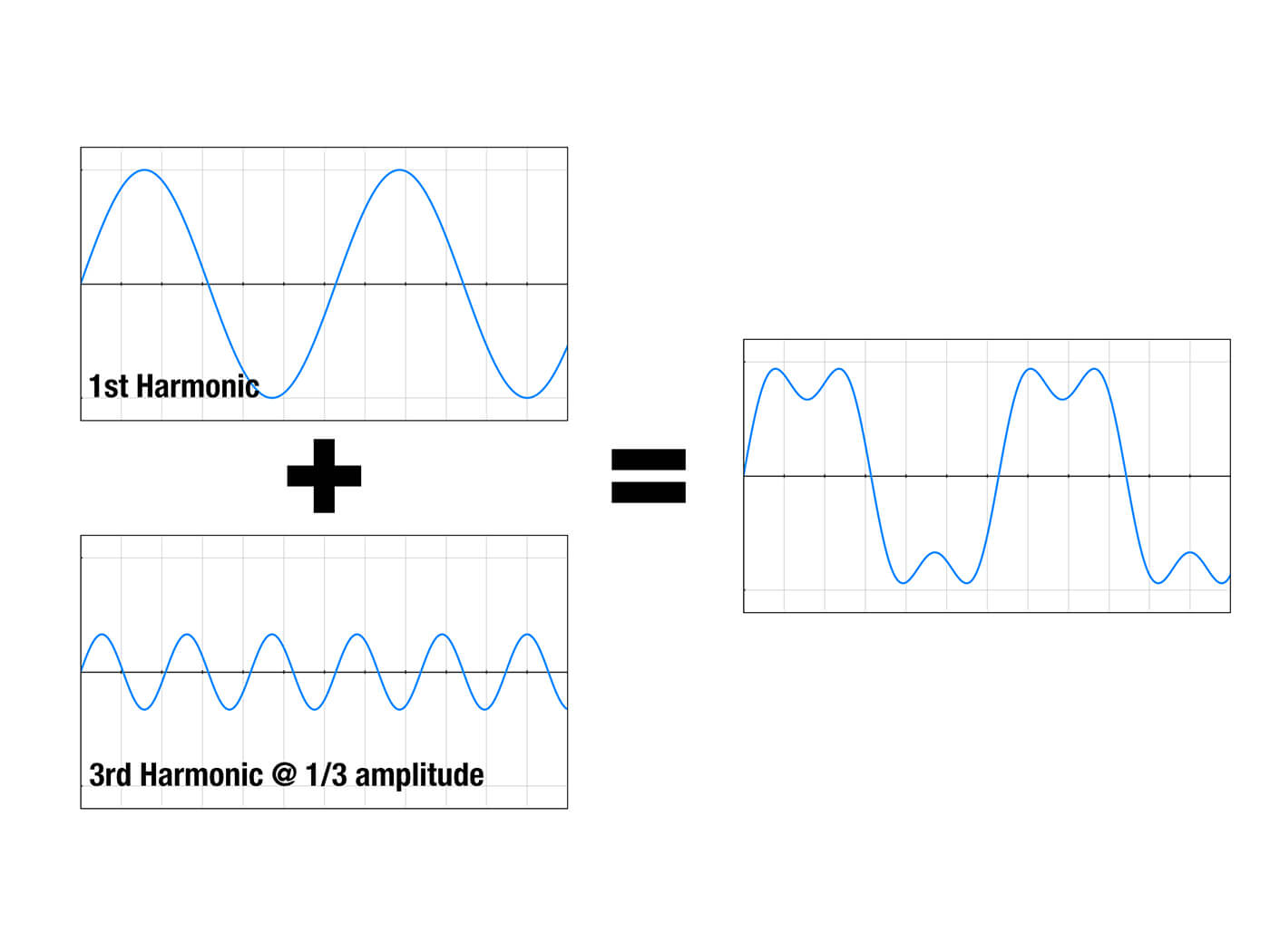
However, in order to construct a perfect square wave in this way you would need to generate an infinite number of partials, which is somewhat impractical, but a close approximation can be created with perhaps six-to-10 partials. 

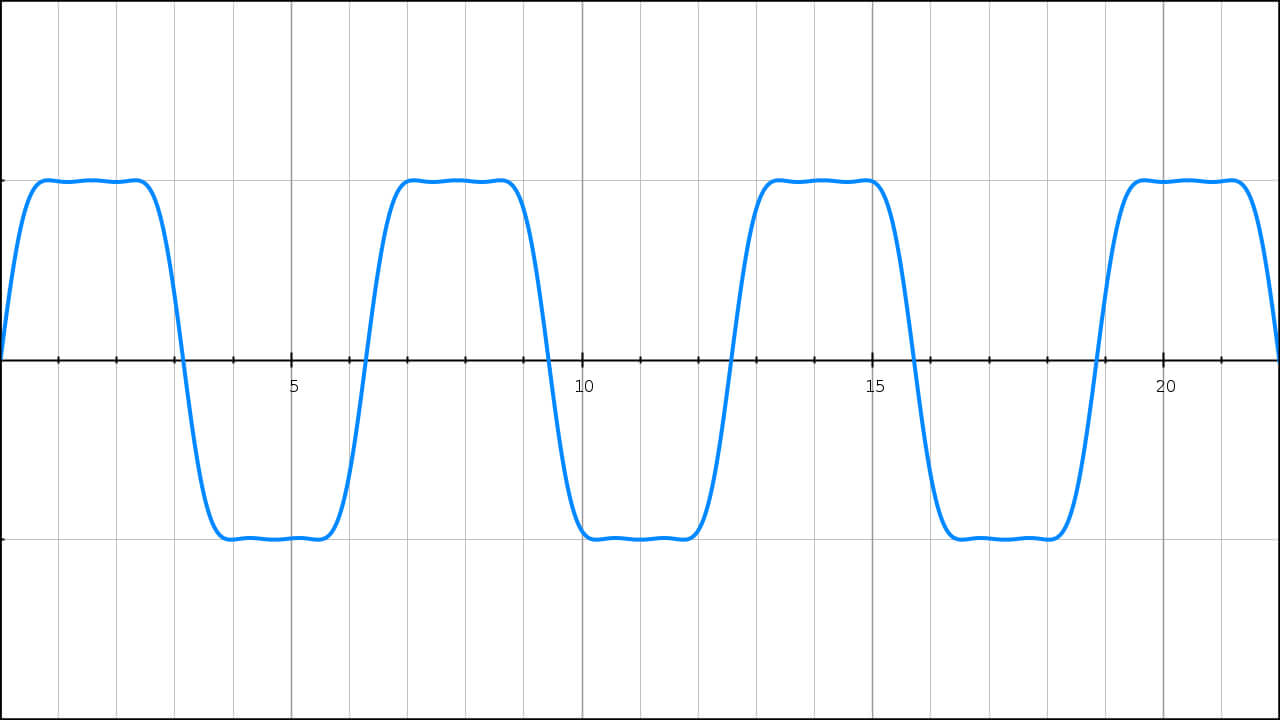
But FM synths don’t mix partials in this way unless using an algorithm made up entirely of carriers. Rather, one operator is used to modulate the frequency of another and this allows FM to create a close approximation of a square wave (or any other basic waveform) using only two sine-wave operators.

Frequency ratio

Each operator has a ‘frequency ratio’ setting that governs the relationship between fundamental frequency and operator frequency; the fundamental frequency is itself determined by the key being played. For example, if you play a middle-A key, the fundamental frequency will be 440Hz. An operator set to a frequency ratio of ‘2’ would therefore produce a frequency of 880Hz.

Modulating a carrier with a ratio of ‘1’ with a modulator with ratio ‘1’ will introduce every harmonic into the carrier. Setting the modulator’s level to around 25% gives a steady decrease in the amplitude of each harmonic. As it happens, this is the recipe for building a sawtooth wave from partials. 

Similarly, with a carrier ratio of ‘1’, a modulator ratio of ‘2’ and modulator level of 75%, every other harmonic (I.E. 1st, 3rd, 5th, etc.) will be introduced into the carrier at a reducing amplitude. You will recall that this is the recipe for a square wave.

The ratio isn’t limited to whole numbers and using fractional values allows you to break away completely from the sorts of timbres a subtractive synth can produce. Added to that, modulation sources, such as per-operator amplitude envelopes, pitch envelopes and LFOs, allow you to introduce variations and subtleties that no subtractive synth could pull off.

There’s no denying the steepness of FM’s learning curve, but once you clear the initial hurdles and develop a sense of how overtones and harmonics impact the timbre of a sound, it becomes a lot easier. FM brings a completely different character of sound to your productions – it is well worth the effort!

Read the history of FM synthesis here.